
Take the square root of both sides of this equation to get:Īdd 2 to both sides of the equation to get:

Subtract from both sides of the equation to get: Once you have succeeded in transforming the equation of a circle into standard form, you need to convert it into graphing form so you can show it on a graph.Īssume the standard form of your equation is: Use of the completing the squares method will also be seen in examples shown further down in this lesson. If you are not familiar with the completing the squares method, you might want to review the following lesson regarding it. This would result in the standard equation of a circle that would be in the form of:ģ is the x-coordinate of the center of the circle.Ģ is the y-coordinate of the center of the circle. Once you did that, you would complete the squares on the x terms and the y terms separately. You would do that by moving the constant over to the right side of the equation and then grouping the x terms together and the y terms together on the left side of the equation until you had something like this: You would need to transform this equation into standard form in order to find the vertex of the circle and the radius of the circle.
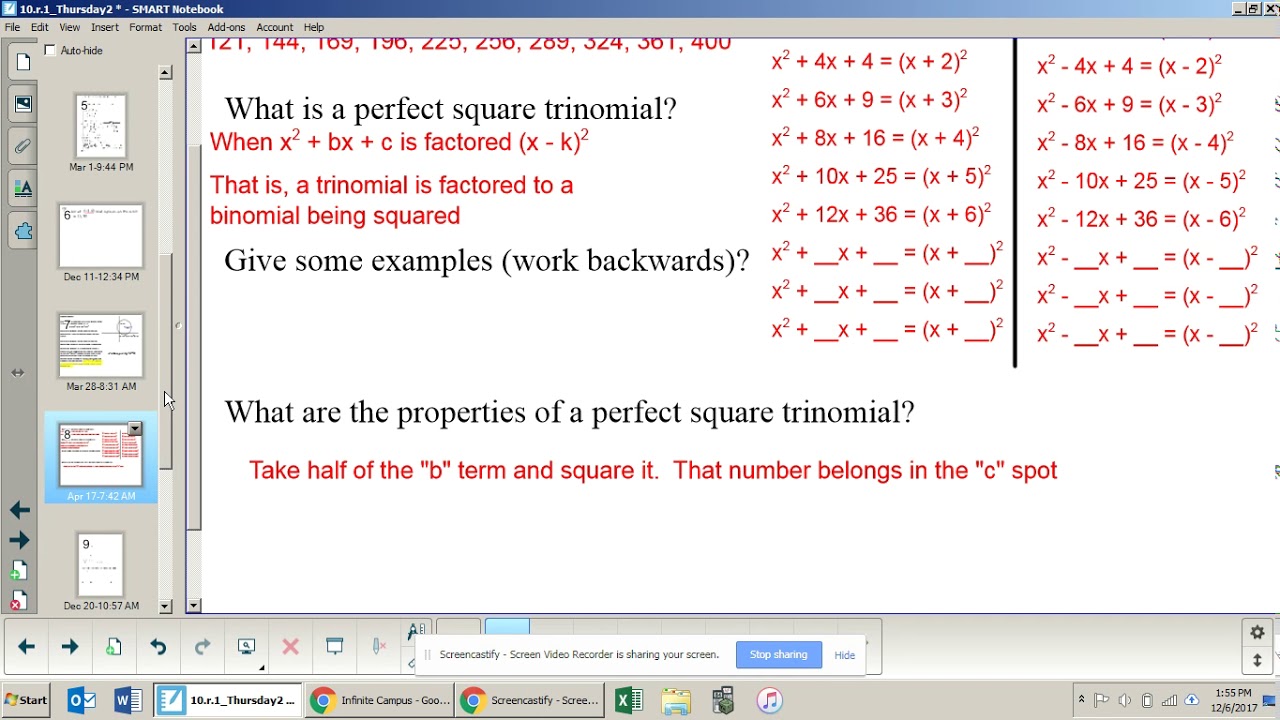
You may also be given the equation of a circle in non-standard form. The center of the circle would be equal to (x,y) = (3,2). The center of the circle is also called the vertex. K is the y-coordinate of the center of the circle. H is the x-coordinate of the center of the circle.
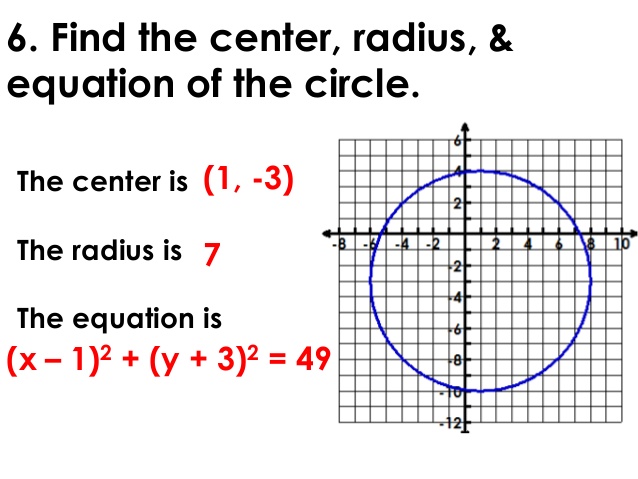
The standard form for the equation of a circle is: This lesson provides an overview of equations involving a circle.


 0 kommentar(er)
0 kommentar(er)
